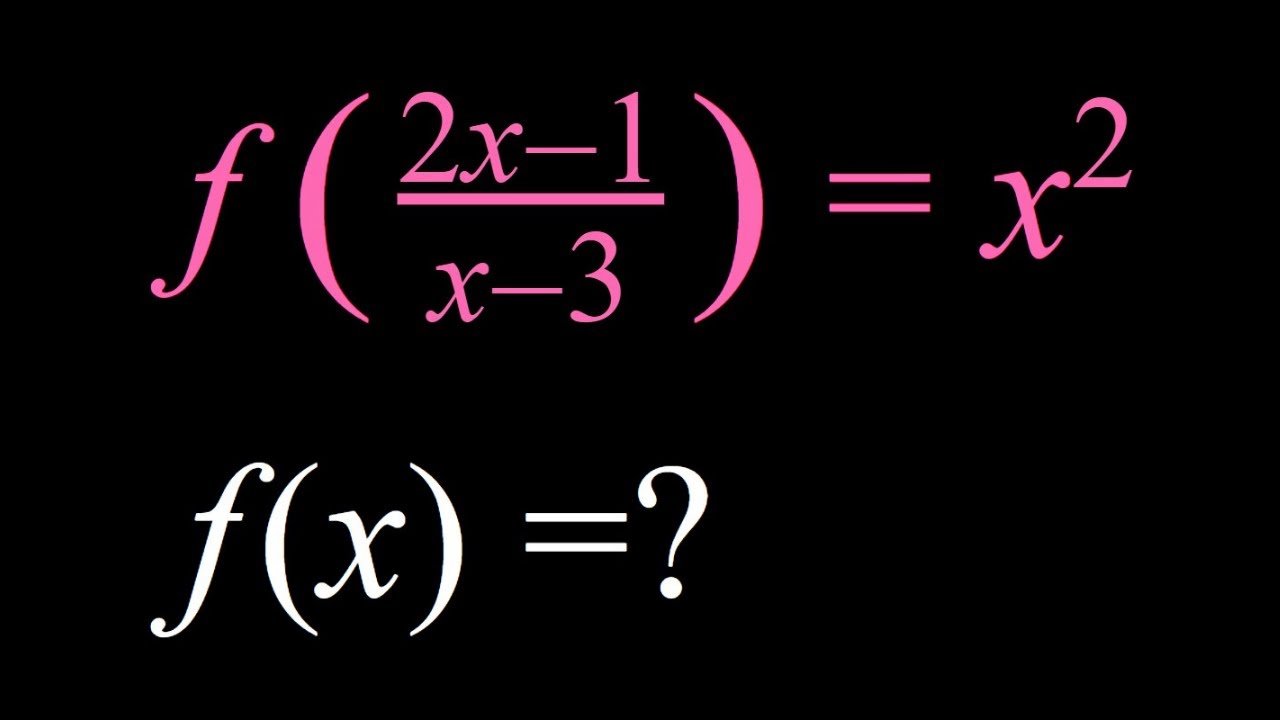Functional Form Math
Functional Form Math - O for example, we could examine math sat score effects by looking at dummies for 500 ≤ satm < 600, 600 ≤ satm < 700, and satm ≥ 701, leaving out. Before we do that, we should note that all of these forms will always include a constant. There are several commonly used function forms we will examine. A functional form refers to the algebraic form of a relationship between a dependent variable and regressors or explanatory variables. Consider the general functional form for the case of two independent variables x 1 and x 2:y = f (x 1, x 2, ε), where y is the dependent variable, x 1 and x 2.
A functional form refers to the algebraic form of a relationship between a dependent variable and regressors or explanatory variables. O for example, we could examine math sat score effects by looking at dummies for 500 ≤ satm < 600, 600 ≤ satm < 700, and satm ≥ 701, leaving out. Before we do that, we should note that all of these forms will always include a constant. There are several commonly used function forms we will examine. Consider the general functional form for the case of two independent variables x 1 and x 2:y = f (x 1, x 2, ε), where y is the dependent variable, x 1 and x 2.
A functional form refers to the algebraic form of a relationship between a dependent variable and regressors or explanatory variables. O for example, we could examine math sat score effects by looking at dummies for 500 ≤ satm < 600, 600 ≤ satm < 700, and satm ≥ 701, leaving out. Before we do that, we should note that all of these forms will always include a constant. Consider the general functional form for the case of two independent variables x 1 and x 2:y = f (x 1, x 2, ε), where y is the dependent variable, x 1 and x 2. There are several commonly used function forms we will examine.
Changing students' attitudes to mathematics improves test scores
Before we do that, we should note that all of these forms will always include a constant. Consider the general functional form for the case of two independent variables x 1 and x 2:y = f (x 1, x 2, ε), where y is the dependent variable, x 1 and x 2. O for example, we could examine math sat.
Kniv Fiskars Functional Form brödbräda och knivuppsättning
Consider the general functional form for the case of two independent variables x 1 and x 2:y = f (x 1, x 2, ε), where y is the dependent variable, x 1 and x 2. A functional form refers to the algebraic form of a relationship between a dependent variable and regressors or explanatory variables. There are several commonly used.
A Quick and Easy Functional Equation YouTube
Consider the general functional form for the case of two independent variables x 1 and x 2:y = f (x 1, x 2, ε), where y is the dependent variable, x 1 and x 2. A functional form refers to the algebraic form of a relationship between a dependent variable and regressors or explanatory variables. Before we do that, we.
72 Choosing a Functional Form
O for example, we could examine math sat score effects by looking at dummies for 500 ≤ satm < 600, 600 ≤ satm < 700, and satm ≥ 701, leaving out. A functional form refers to the algebraic form of a relationship between a dependent variable and regressors or explanatory variables. Before we do that, we should note that all.
PPT An Introduction to Logistic Regression PowerPoint Presentation
Consider the general functional form for the case of two independent variables x 1 and x 2:y = f (x 1, x 2, ε), where y is the dependent variable, x 1 and x 2. There are several commonly used function forms we will examine. O for example, we could examine math sat score effects by looking at dummies for.
Functional Maths Level 1 Teaching Resources
Consider the general functional form for the case of two independent variables x 1 and x 2:y = f (x 1, x 2, ε), where y is the dependent variable, x 1 and x 2. There are several commonly used function forms we will examine. Before we do that, we should note that all of these forms will always include.
CrunchEconometrix A StepbyStep Tutorial on Research and Data Analysis
A functional form refers to the algebraic form of a relationship between a dependent variable and regressors or explanatory variables. O for example, we could examine math sat score effects by looking at dummies for 500 ≤ satm < 600, 600 ≤ satm < 700, and satm ≥ 701, leaving out. Consider the general functional form for the case of.
Kniv Fiskars Functional Form brödbräda och knivuppsättning
Consider the general functional form for the case of two independent variables x 1 and x 2:y = f (x 1, x 2, ε), where y is the dependent variable, x 1 and x 2. There are several commonly used function forms we will examine. O for example, we could examine math sat score effects by looking at dummies for.
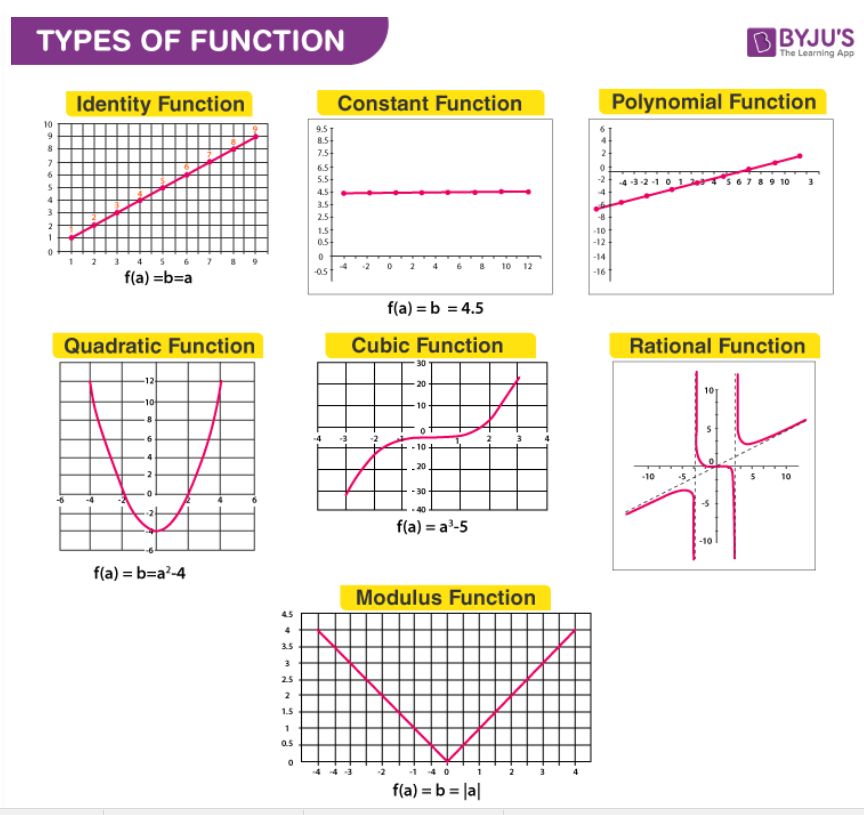
Functions Definition, Types, Domain Range and Video Lesson
A functional form refers to the algebraic form of a relationship between a dependent variable and regressors or explanatory variables. There are several commonly used function forms we will examine. Consider the general functional form for the case of two independent variables x 1 and x 2:y = f (x 1, x 2, ε), where y is the dependent variable,.
13 Functional Forms Examples of Choosing Functional Forms
Before we do that, we should note that all of these forms will always include a constant. O for example, we could examine math sat score effects by looking at dummies for 500 ≤ satm < 600, 600 ≤ satm < 700, and satm ≥ 701, leaving out. Consider the general functional form for the case of two independent variables.
There Are Several Commonly Used Function Forms We Will Examine.
A functional form refers to the algebraic form of a relationship between a dependent variable and regressors or explanatory variables. Before we do that, we should note that all of these forms will always include a constant. Consider the general functional form for the case of two independent variables x 1 and x 2:y = f (x 1, x 2, ε), where y is the dependent variable, x 1 and x 2. O for example, we could examine math sat score effects by looking at dummies for 500 ≤ satm < 600, 600 ≤ satm < 700, and satm ≥ 701, leaving out.