Mapping Math Definition

Mapping Math Definition - These terms may have originated as from the process of making a. Mapping, any prescribed way of assigning to each object in one set a particular object in another (or the same) set. Mapping applies to any set: In mathematics, a map or mapping is a function in its general sense. In mathematics, mapping refers to a relation that associates each element of one set with exactly one element of another set.

In mathematics, a map or mapping is a function in its general sense. These terms may have originated as from the process of making a. In mathematics, mapping refers to a relation that associates each element of one set with exactly one element of another set. Mapping, any prescribed way of assigning to each object in one set a particular object in another (or the same) set. Mapping applies to any set:

In mathematics, mapping refers to a relation that associates each element of one set with exactly one element of another set. Mapping, any prescribed way of assigning to each object in one set a particular object in another (or the same) set. In mathematics, a map or mapping is a function in its general sense. Mapping applies to any set: These terms may have originated as from the process of making a.

Relation Math Example

Mapping, any prescribed way of assigning to each object in one set a particular object in another (or the same) set. These terms may have originated as from the process of making a. In mathematics, mapping refers to a relation that associates each element of one set with exactly one element of another set. Mapping applies to any set: In.

Mapping Diagrams Definition, Examples, Creating & Types (2023)

In mathematics, a map or mapping is a function in its general sense. These terms may have originated as from the process of making a. Mapping applies to any set: Mapping, any prescribed way of assigning to each object in one set a particular object in another (or the same) set. In mathematics, mapping refers to a relation that associates.

$Mapping math 5 ways to use concept maps in the math classroom Teach$

Mapping math 5 ways to use concept maps in the math classroom Teach

These terms may have originated as from the process of making a. Mapping, any prescribed way of assigning to each object in one set a particular object in another (or the same) set. In mathematics, mapping refers to a relation that associates each element of one set with exactly one element of another set. In mathematics, a map or mapping.

Mapping Diagrams Definition, Examples, Creating & Types (2023)

Mapping applies to any set: In mathematics, mapping refers to a relation that associates each element of one set with exactly one element of another set. These terms may have originated as from the process of making a. In mathematics, a map or mapping is a function in its general sense. Mapping, any prescribed way of assigning to each object.

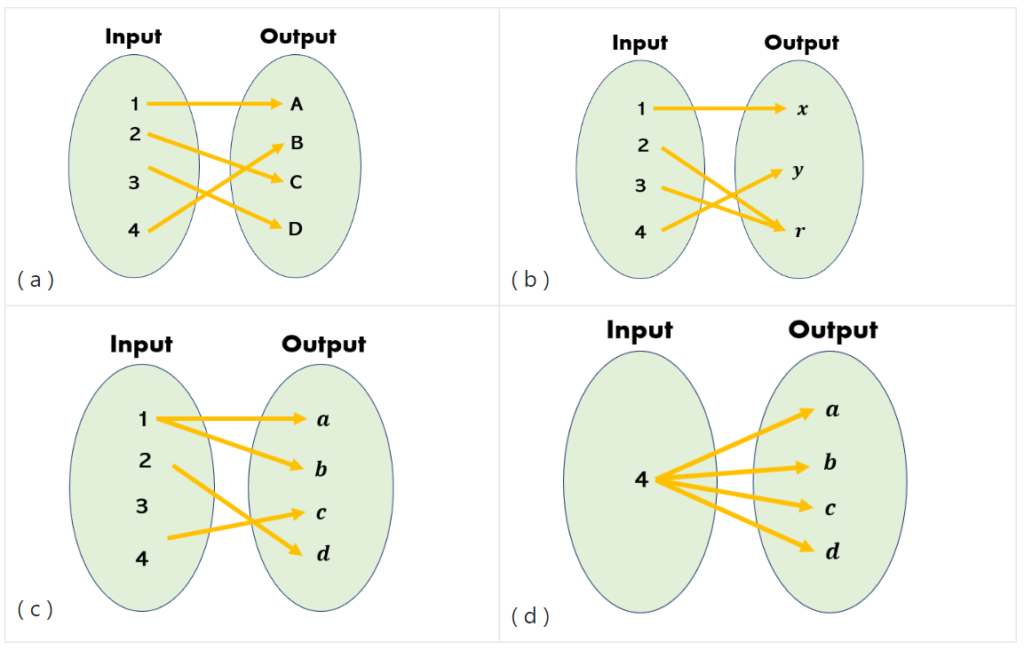
Ordered Pairs Function Examples

Mapping, any prescribed way of assigning to each object in one set a particular object in another (or the same) set. In mathematics, a map or mapping is a function in its general sense. These terms may have originated as from the process of making a. Mapping applies to any set: In mathematics, mapping refers to a relation that associates.

Part 3 Functional Mapping Further Functions and Relations

Mapping applies to any set: In mathematics, a map or mapping is a function in its general sense. Mapping, any prescribed way of assigning to each object in one set a particular object in another (or the same) set. In mathematics, mapping refers to a relation that associates each element of one set with exactly one element of another set..

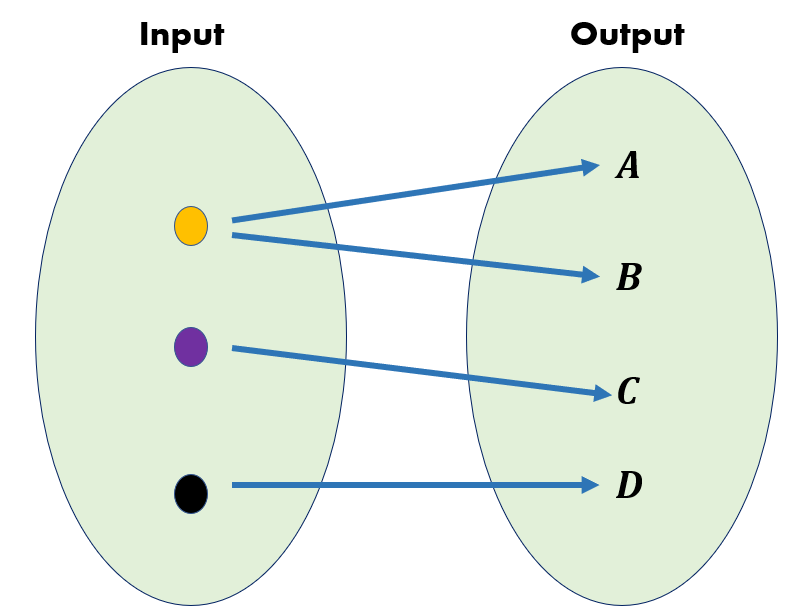
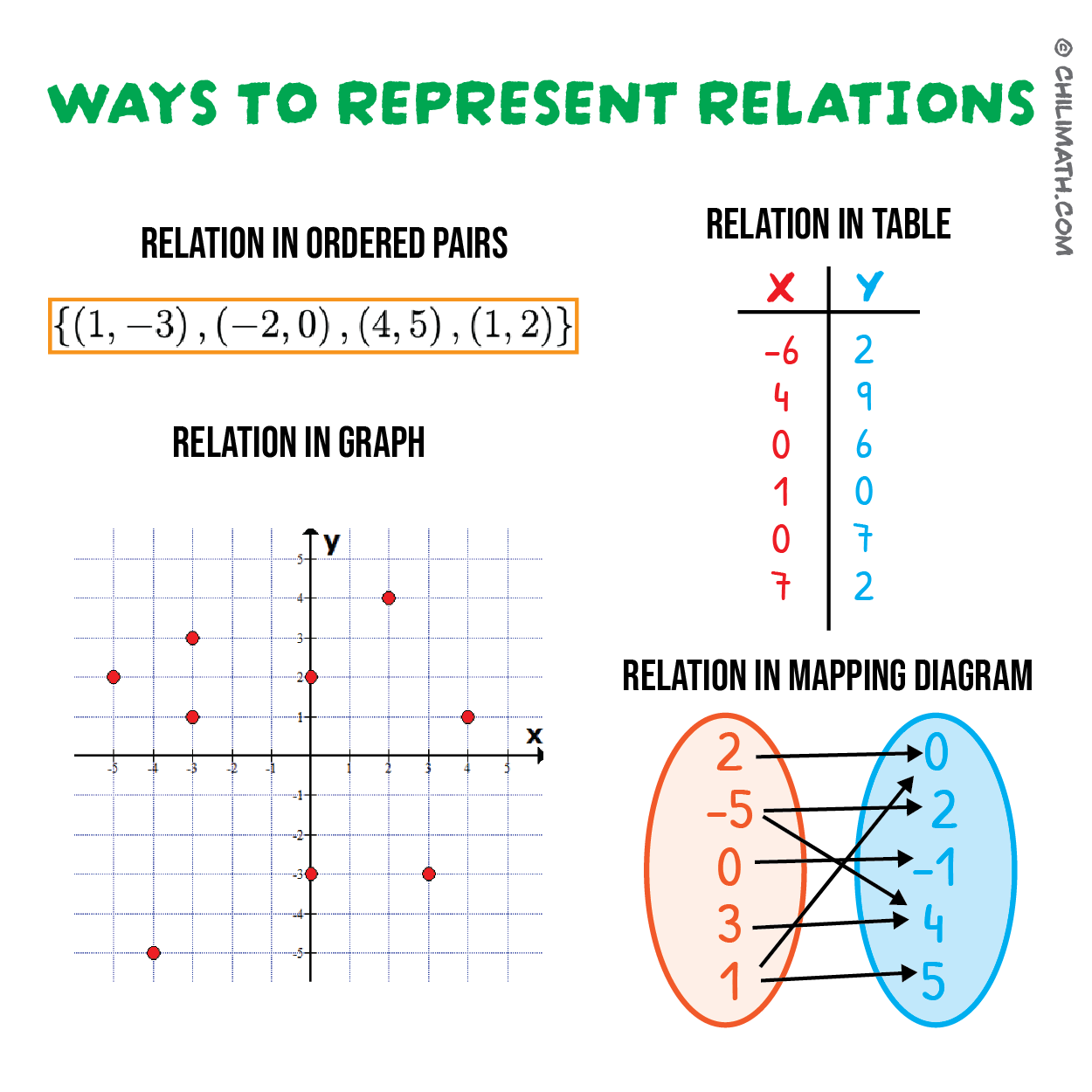
[DIAGRAM] Mathematical Mapping Diagram

In mathematics, mapping refers to a relation that associates each element of one set with exactly one element of another set. These terms may have originated as from the process of making a. Mapping applies to any set: In mathematics, a map or mapping is a function in its general sense. Mapping, any prescribed way of assigning to each object.

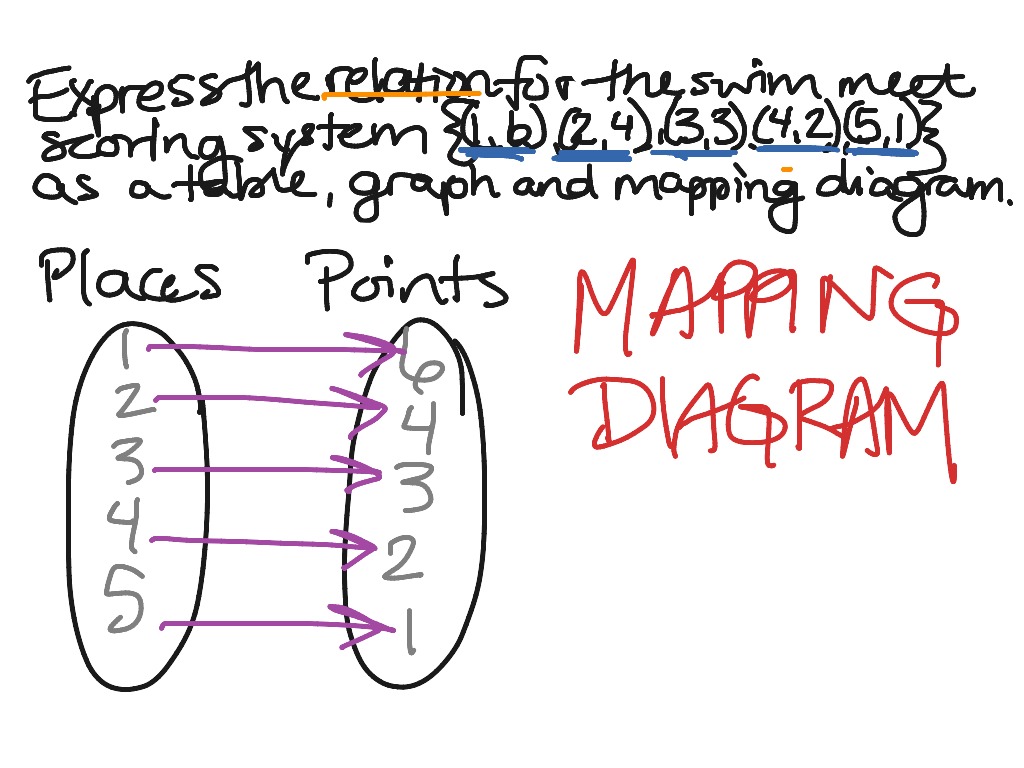
42 Relations and Functions Tables, Graphs, and Mapping Diagrams

In mathematics, a map or mapping is a function in its general sense. In mathematics, mapping refers to a relation that associates each element of one set with exactly one element of another set. Mapping applies to any set: These terms may have originated as from the process of making a. Mapping, any prescribed way of assigning to each object.

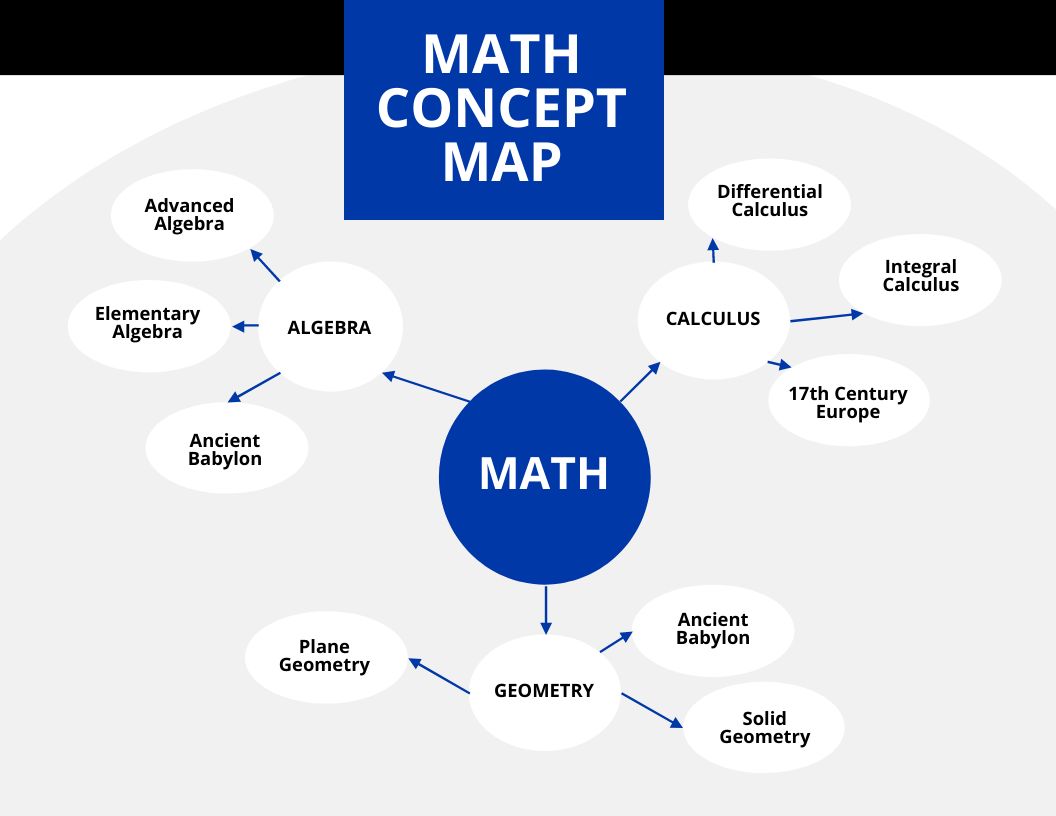
$Math Concept Map Template in Word, Google Docs Download$

Math Concept Map Template in Word, Google Docs Download

Mapping, any prescribed way of assigning to each object in one set a particular object in another (or the same) set. In mathematics, mapping refers to a relation that associates each element of one set with exactly one element of another set. These terms may have originated as from the process of making a. Mapping applies to any set: In.

Mathematics Definition

These terms may have originated as from the process of making a. In mathematics, a map or mapping is a function in its general sense. In mathematics, mapping refers to a relation that associates each element of one set with exactly one element of another set. Mapping, any prescribed way of assigning to each object in one set a particular.

Mapping, Any Prescribed Way Of Assigning To Each Object In One Set A Particular Object In Another (Or The Same) Set.

In mathematics, a map or mapping is a function in its general sense. Mapping applies to any set: In mathematics, mapping refers to a relation that associates each element of one set with exactly one element of another set. These terms may have originated as from the process of making a.