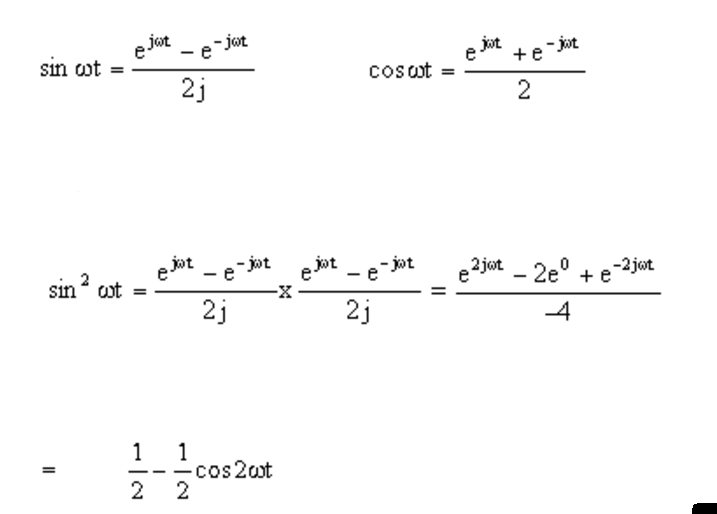
Sin And Cos In Exponential Form
Sin And Cos In Exponential Form - From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. These formulas allow us to define sin and cos for complex inputs. We can also express the trig functions in terms of the complex exponentials eit; Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever value of. The existence of these formulas allows us to solve 2 nd order differential. E¡it since we know that cos(t) is even in t and sin(t) is odd in t.
E¡it since we know that cos(t) is even in t and sin(t) is odd in t. The existence of these formulas allows us to solve 2 nd order differential. Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever value of. These formulas allow us to define sin and cos for complex inputs. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. We can also express the trig functions in terms of the complex exponentials eit;
The existence of these formulas allows us to solve 2 nd order differential. E¡it since we know that cos(t) is even in t and sin(t) is odd in t. Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever value of. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. These formulas allow us to define sin and cos for complex inputs. We can also express the trig functions in terms of the complex exponentials eit;
Question Video Converting the Product of Complex Numbers in Polar Form
From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. These formulas allow us to define sin and cos for complex inputs. The existence of these formulas allows us to solve 2 nd order differential. Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine.
FileSine Cosine Exponential qtl1.svg Wikimedia Commons Math
These formulas allow us to define sin and cos for complex inputs. E¡it since we know that cos(t) is even in t and sin(t) is odd in t. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. We can also express the trig functions in terms of the complex exponentials.
Exponential Form of Complex Numbers
From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. The existence of these formulas allows us to solve 2 nd order differential. Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever value of. E¡it since we know that cos(t) is even.
A Trigonometric Exponential Equation with Sine and Cosine Math
The existence of these formulas allows us to solve 2 nd order differential. We can also express the trig functions in terms of the complex exponentials eit; From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. These formulas allow us to define sin and cos for complex inputs. Technically, you.
Euler's exponential values of Sine and Cosine Exponential values of
Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever value of. E¡it since we know that cos(t) is even in t and sin(t) is odd in t. The existence of these formulas allows us to solve 2 nd order differential. We can also express the trig functions in terms of the.
Expressing Various Complex Numbers in Exponential Form Tim Gan Math
Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever value of. The existence of these formulas allows us to solve 2 nd order differential. We can also express the trig functions in terms of the complex exponentials eit; E¡it since we know that cos(t) is even in t and sin(t) is.
e^x=cos(x)+i sin(x). Where does that exponential form of complex
Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever value of. We can also express the trig functions in terms of the complex exponentials eit; The existence of these formulas allows us to solve 2 nd order differential. These formulas allow us to define sin and cos for complex inputs. E¡it.
QPSK modulation and generating signals
Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever value of. The existence of these formulas allows us to solve 2 nd order differential. E¡it since we know that cos(t) is even in t and sin(t) is odd in t. We can also express the trig functions in terms of the.
Question Video Converting Complex Numbers from Polar to Exponential
The existence of these formulas allows us to solve 2 nd order differential. These formulas allow us to define sin and cos for complex inputs. E¡it since we know that cos(t) is even in t and sin(t) is odd in t. We can also express the trig functions in terms of the complex exponentials eit; From these relations and the.
Complex Numbers 4/4 Cos and Sine to Complex Exponential YouTube
E¡it since we know that cos(t) is even in t and sin(t) is odd in t. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. These formulas allow us to define sin and cos for complex inputs. The existence of these formulas allows us to solve 2 nd order differential..
E¡It Since We Know That Cos(T) Is Even In T And Sin(T) Is Odd In T.
These formulas allow us to define sin and cos for complex inputs. We can also express the trig functions in terms of the complex exponentials eit; Technically, you can use the maclaurin series of the exponential function to evaluate sine and cosine at whatever value of. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that.