The Segments Shown Below Could Form A Triangle

The Segments Shown Below Could Form A Triangle - Let's check if this condition is. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. A triangle cannot have a perimeter of length zero. The segments shown below could form a triangle. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. These segments could potentially form a triangle.

A triangle cannot have a perimeter of length zero. These segments could potentially form a triangle. Let's check if this condition is. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. The segments shown below could form a triangle.

To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. A triangle cannot have a perimeter of length zero. The segments shown below could form a triangle. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. These segments could potentially form a triangle. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. Let's check if this condition is.

The segments shown below could form a triangle. A с B 3 6 B C A O A

The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. The segments shown below could form a triangle. These segments could potentially form a triangle. A triangle cannot have a perimeter of length zero. To form a triangle, the sum of the lengths of any two sides must.

SOLVED 'The segments shown below could form a triangle. The segments

The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. Let's check if this condition is. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. The segments shown below could form a triangle. These segments could.

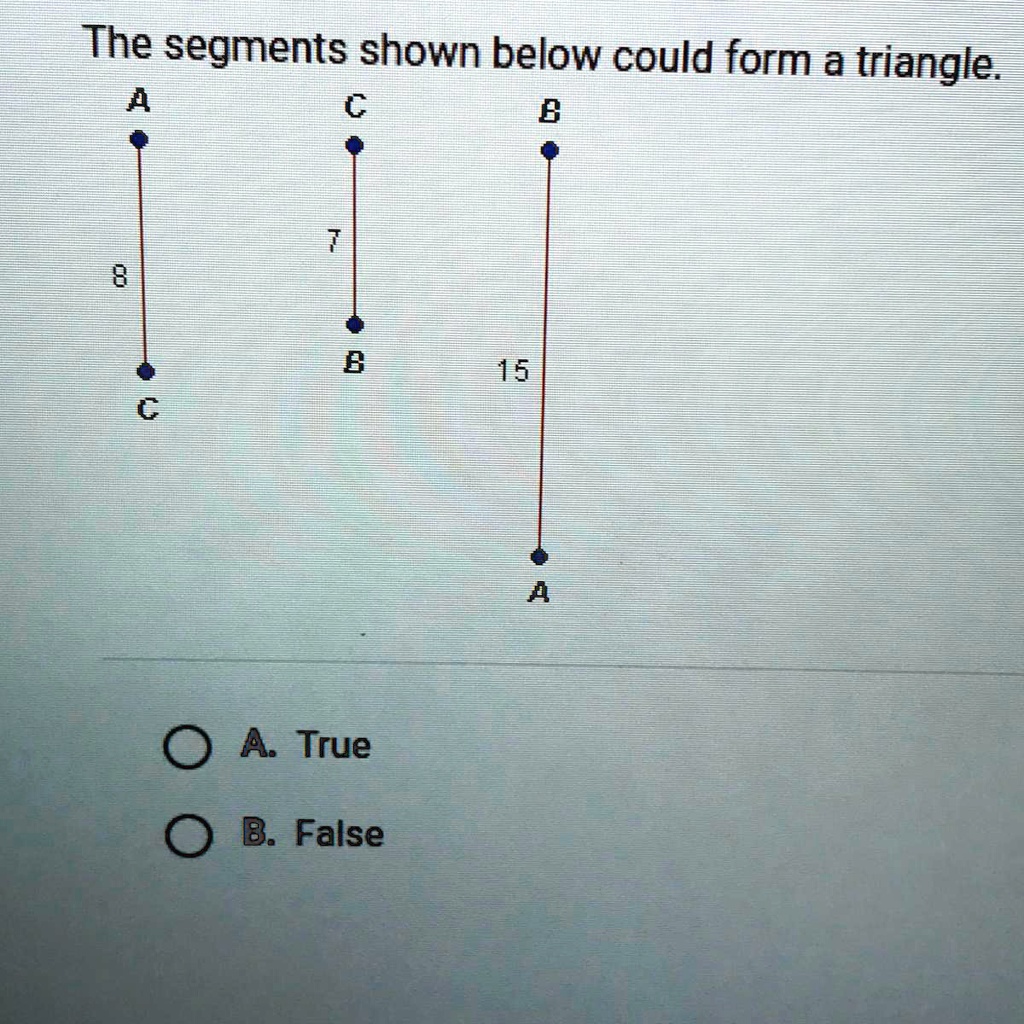
The segments shown below could form a triangle. A. True B. False

To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. These segments could potentially form a triangle. The segments shown below could form a triangle. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the..

The segments shown below could form a triangle.

A triangle cannot have a perimeter of length zero. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. Let's check if this condition is. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. These.

The segments shown below could form a triangle. д C B 9 11 B C O A

For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. These segments could potentially form a triangle. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle.

The segments shown below could form a triangle. А С B 5 6 В 12 O A

For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. A triangle cannot have a perimeter of length zero. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. These segments could potentially form a triangle. To.

The segments shown below could form a triangle. True or False

For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. A triangle cannot have a perimeter of length zero. Let's check if this condition is. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. The.

the segments shown below could form a triangle ac9 cb7 ba16

To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. Let's check if this condition is. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality.

The segments shown below could form a triangle.True or False

A triangle cannot have a perimeter of length zero. These segments could potentially form a triangle. The segments shown below could form a triangle. Let's check if this condition is. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side.

The segments shown below could form a triangle. OA. True OB. False

The segments shown below could form a triangle. These segments could potentially form a triangle. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. To form.

The Lengths Given (Ac=6, Cb=5, Ba=8) Satisfy The Triangle Inequality Theorem As The Sum Of Any Two Sides Is Greater Than The.

A triangle cannot have a perimeter of length zero. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. These segments could potentially form a triangle. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be.