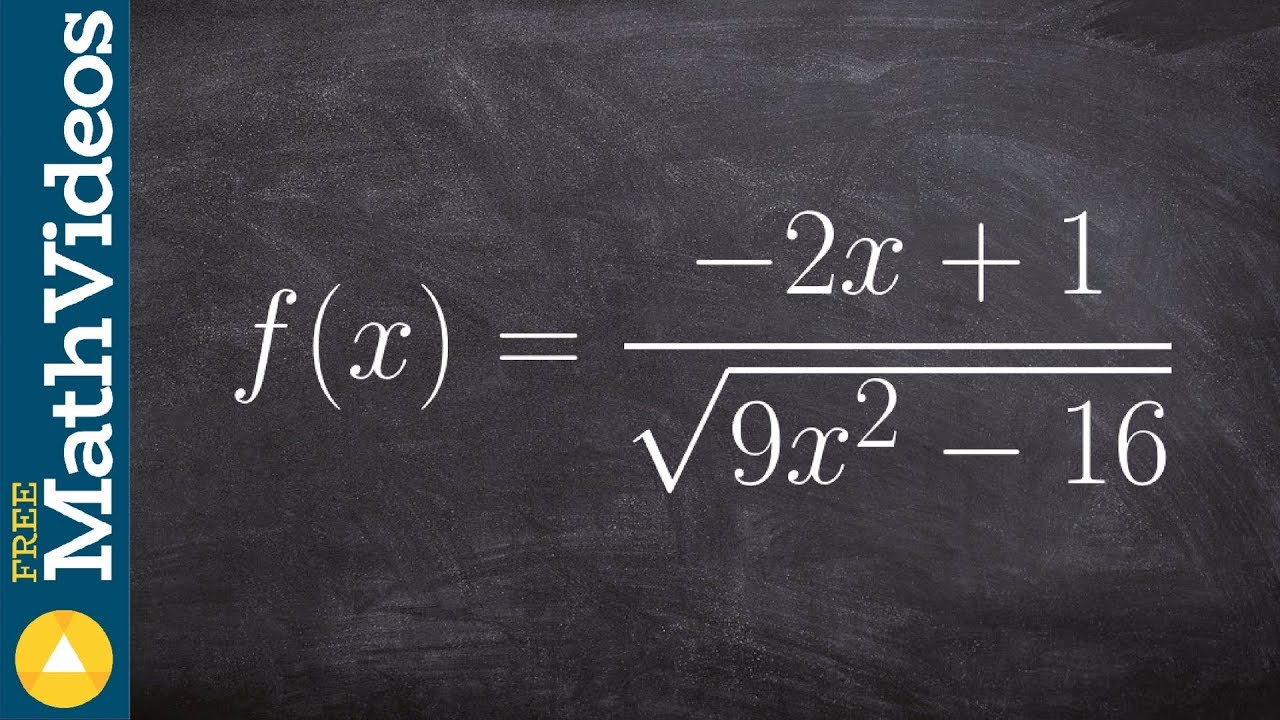What Is The Square Root Of Infinity
What Is The Square Root Of Infinity - The square of infinity can be expressed as the following limit, we can get \[\mathop {\lim }\limits_{x \to \infty } \sqrt x = + \infty \] hence, the square. An example of an infinite. For example, \(4 + 7 = 11\). Thus both the square root of infinity and square of infinity make sense when infinity is interpreted as a hyperreal number. The answer is infinity (∞) to any power. So, let’s start thinking about addition with infinity. Learn how to evaluate square root of infinity (√∞) in calculus with mathway's free math problem solver.
So, let’s start thinking about addition with infinity. Learn how to evaluate square root of infinity (√∞) in calculus with mathway's free math problem solver. The answer is infinity (∞) to any power. For example, \(4 + 7 = 11\). The square of infinity can be expressed as the following limit, we can get \[\mathop {\lim }\limits_{x \to \infty } \sqrt x = + \infty \] hence, the square. Thus both the square root of infinity and square of infinity make sense when infinity is interpreted as a hyperreal number. An example of an infinite.
Thus both the square root of infinity and square of infinity make sense when infinity is interpreted as a hyperreal number. An example of an infinite. The answer is infinity (∞) to any power. Learn how to evaluate square root of infinity (√∞) in calculus with mathway's free math problem solver. So, let’s start thinking about addition with infinity. For example, \(4 + 7 = 11\). The square of infinity can be expressed as the following limit, we can get \[\mathop {\lim }\limits_{x \to \infty } \sqrt x = + \infty \] hence, the square.
Evaluate the limit at infinity with square root YouTube
Thus both the square root of infinity and square of infinity make sense when infinity is interpreted as a hyperreal number. The square of infinity can be expressed as the following limit, we can get \[\mathop {\lim }\limits_{x \to \infty } \sqrt x = + \infty \] hence, the square. For example, \(4 + 7 = 11\). An example of.
The square root of infinity (Infinity part 1) sheet music for Piano
The answer is infinity (∞) to any power. So, let’s start thinking about addition with infinity. For example, \(4 + 7 = 11\). The square of infinity can be expressed as the following limit, we can get \[\mathop {\lim }\limits_{x \to \infty } \sqrt x = + \infty \] hence, the square. Thus both the square root of infinity and.
The Conjugate Trick with a Square Root and Limits at Infinity (as x
Thus both the square root of infinity and square of infinity make sense when infinity is interpreted as a hyperreal number. Learn how to evaluate square root of infinity (√∞) in calculus with mathway's free math problem solver. An example of an infinite. The square of infinity can be expressed as the following limit, we can get \[\mathop {\lim }\limits_{x.
Limits at infinity of quotients with square roots (even power) AP
Thus both the square root of infinity and square of infinity make sense when infinity is interpreted as a hyperreal number. So, let’s start thinking about addition with infinity. Learn how to evaluate square root of infinity (√∞) in calculus with mathway's free math problem solver. The square of infinity can be expressed as the following limit, we can get.
Limit at Infinity with Square Root in the Numerator Calculus Math
The answer is infinity (∞) to any power. The square of infinity can be expressed as the following limit, we can get \[\mathop {\lim }\limits_{x \to \infty } \sqrt x = + \infty \] hence, the square. Thus both the square root of infinity and square of infinity make sense when infinity is interpreted as a hyperreal number. So, let’s.
Limit of Square Root Function at Infinity with Rationalisation and
The square of infinity can be expressed as the following limit, we can get \[\mathop {\lim }\limits_{x \to \infty } \sqrt x = + \infty \] hence, the square. Thus both the square root of infinity and square of infinity make sense when infinity is interpreted as a hyperreal number. So, let’s start thinking about addition with infinity. For example,.
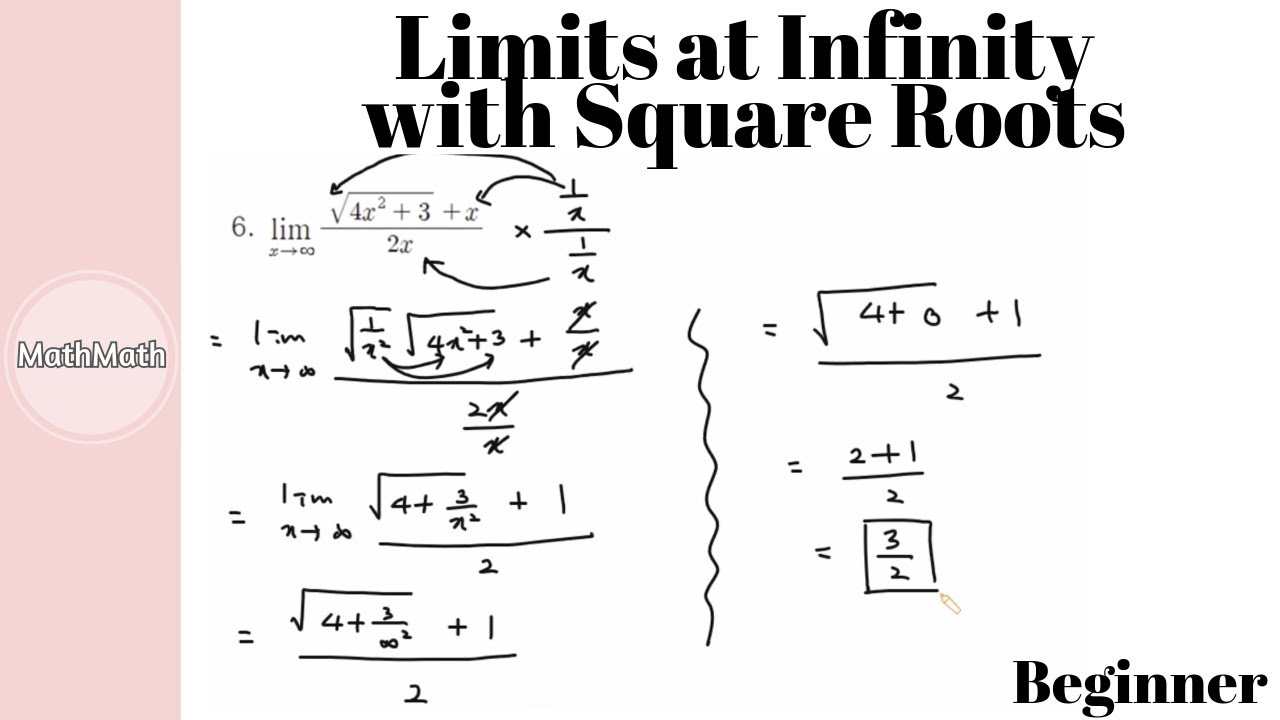
Calculus HOW TO Limits at Infinity with Square Roots (Beginner Level
The answer is infinity (∞) to any power. Learn how to evaluate square root of infinity (√∞) in calculus with mathway's free math problem solver. So, let’s start thinking about addition with infinity. For example, \(4 + 7 = 11\). Thus both the square root of infinity and square of infinity make sense when infinity is interpreted as a hyperreal.
Can You Solve This? Infinite Radicals Math competition, Mathematics
Learn how to evaluate square root of infinity (√∞) in calculus with mathway's free math problem solver. Thus both the square root of infinity and square of infinity make sense when infinity is interpreted as a hyperreal number. An example of an infinite. The answer is infinity (∞) to any power. For example, \(4 + 7 = 11\).
Square root infinite series questions Simplification Uwelearn YouTube
An example of an infinite. Thus both the square root of infinity and square of infinity make sense when infinity is interpreted as a hyperreal number. For example, \(4 + 7 = 11\). The answer is infinity (∞) to any power. Learn how to evaluate square root of infinity (√∞) in calculus with mathway's free math problem solver.
Calculus Limits at Infinity with Square Roots Calculus, Math videos
The square of infinity can be expressed as the following limit, we can get \[\mathop {\lim }\limits_{x \to \infty } \sqrt x = + \infty \] hence, the square. So, let’s start thinking about addition with infinity. The answer is infinity (∞) to any power. For example, \(4 + 7 = 11\). Learn how to evaluate square root of infinity.
Learn How To Evaluate Square Root Of Infinity (√∞) In Calculus With Mathway's Free Math Problem Solver.
An example of an infinite. Thus both the square root of infinity and square of infinity make sense when infinity is interpreted as a hyperreal number. So, let’s start thinking about addition with infinity. For example, \(4 + 7 = 11\).
The Answer Is Infinity (∞) To Any Power.
The square of infinity can be expressed as the following limit, we can get \[\mathop {\lim }\limits_{x \to \infty } \sqrt x = + \infty \] hence, the square.